主题：【原创】值得玩味的珠峰高程

值得玩味的珠峰高程

武汉大学 叶晓明

    我曾多次用珠峰高程的结果为案例来质疑现有测量理论的误差分类学说。我之所以用这一案例，一者因为这一案例的知名度高，二者期望达到以子之矛攻子之盾的功效，以减轻我的论述工作量。现在通过网络等多渠道的反馈，越来越觉得这个案例很值得玩味了。
    这个案例是这样的。2005年国家测绘局给出珠峰高程测量结果为8844.43米，精度（标准偏差）为±0.21米。我的意图是，一方面用精度与随机误差的对应逻辑证明珠峰高程的误差是随机误差，另一方面用误差的定义（结果与真值之差）证明珠峰高程的误差是恒定的偏差，应该属于系统误差，从而展示现有测量理论的基本概念逻辑无法自圆其说。现在总结起来，对这个标准偏差±0.21米和珠峰高程误差的关系的理解大体有三种：
1、珠峰高程结果的误差是个恒定的偏差，±0.21米表达这个偏差的可能存在区间的评价，是偏差值的不可确定的程度。这个偏差不存在系统误差、随机误差的分类问题。
2、珠峰高程结果的误差是个随机误差，±0.21米表达这个随机误差的随机变化范围。
3、珠峰高程结果的误差是个恒定的偏差，也是随机误差，±0.21米表达未来相同测量条件下重复测量时测量结果的发散度。
    那么，在这三种答案中，您支持哪一种解释呢？
    如果您支持第一种答案，那么很遗憾地告诉您：您不太可能是一个受过专业训练的测量学者。因为支持这一解释的基本都来自非测量专业人士，当年看到珠峰测量的新闻报道时非测量专业人士一般都是这么理解的。
    如果您支持第2或第3答案，那么您很可能是一个受过专业训练的测量专业人士，对课本的概念逻辑具有较好的记忆，甚至是知名学者。因为测量教科书清楚地写着精度是重复测量结果的发散度，是对随机误差的评价，支持这二答案的基本都是测量专业人士。
    正确的答案只能有一个，那么是谁呢？
    珠峰案例虽然知名度高，但测量过程太复杂，而其答案之一还涉及重复测量的过程，大家自然容易陷入思维死角（实际上这个案例根本就不需要追究其测量过程）。既然如此，我就换个简单的案例。
    作者用数显卡尺测量一钢珠的直径为5.00毫米，根据卡尺的标称计量指标推算出标准偏差为±0.023毫米。现在对标准偏差±0.023毫米有三种解释：
1、 钢珠的直径结果的误差是个恒定的偏差，±0.023毫米表达这个偏差的可能存在区间的评价，是偏差值的不可确定的程度。这个偏差不存在系统误差、随机误差的分类问题。
2、 钢珠的直径结果的误差是个随机误差，±0.023毫米表达这个随机误差的随机变化范围。
3、 钢珠的直径结果的误差是个恒定的偏差，也是随机误差，±0.023毫米表达在未来相同测量条件下重复测量时测量结果的发散度。
    学者优先吧，现看第3种解释——未来相同测量条件下重复测量时测量结果的发散度。这很简单，拿卡尺在相同测量条件重复测量试试呗，您也可以亲自实验做一做。您一定会发现，实验结论非常令人失望，发散度比±0.023毫米小得多，甚至基本就是±0.000毫米。这种解释与事实不符。
    再看第2种解释——随机误差的随机变化范围。这也很简单，既然误差是结果与真值之差，结果是不变的，误差是随机变化的，那么钢珠直径的真值（实际值）就是随机变化的，±0.023毫米的随机变化用手就能摸到。用得着摸吗？傻呀？支持钢珠直径随机变化的能量从哪里来？真能通过测量获得这种无中生有的能量来源那还不发财呀？
    啊啊，只剩下第1种解释了啊，实际上也恰恰就是第1种解释正确。现在我就从数学角度推证一下。。
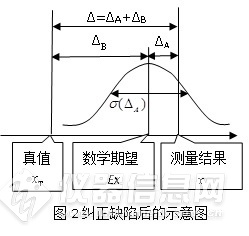
    现有误差序列{△x_i}的数学期望为0，某偏差△x是序列{△x_i}中的一个成员，或者说，序列{△x_i}是偏差△x的所有可能取值的集合。这样，序列{△x_i}的方差σ²(△x)----序列{△x_i}的发散性，就是偏差△x所存在的概率区间的评价值。即

    现在有一个离散的重复观测值序列{x_i}，取其中的某一个x_i作为最终测量结果x。这样，测量结果x与其数学期望Ex之间的偏差△x=x-Ex就是误差序列{△x_i}={x_i-Ex}中的一个成员，而序列{△x_i}={x_i-Ex}的数学期望也正好为0，因为E△x=E(x-Ex)=Ex-Ex=0。这样将△x=x-Ex代入上式就有：

    就是说，测量结果x与其数学期望Ex之间的偏差△x=x-Ex存在于一个数学期望为0、标准偏差为σ(△x)的概率区间内，标准偏差σ(△x)是一个偏差△x=x-Ex的概率区间的评价值！标准偏差原来是一个误差的存在范围的概念，表达测量者主观对一个误差的不可确定的程度---不确定度！就是说，方差是误差的方差，而不是测量结果的方差，跟测量结果x没有直接关系。这就和现有教科书用公式σ²(x)=E(x-Ex)²把方差解释成测量结果x的发散度有所不同了。
    当然，如果以n个不同的x_i的平均值作为最终测量结果x，这时的σ(△x)还将下降根号n倍。
    同样的道理，数学期望与真值之差Ex-x_T也有它的标准偏差，因为它也是测量产生的，追寻到它的上游测量也可以获得其标准偏差(概率范围)。这样，测量结果的总误差的标准偏差自然按照概率法则合成即可获得。
    偏差x-Ex和Ex-x_T都是恒定的偏差，都有标准偏差，没有性质差异，不存在误差分类的问题。数学推理证明，这种新的方差概念解释对贝塞尔公式、最小二乘法等没有任何影响，但测量误差理论的解释中却不需要精度、准确度概念了，不确定度也不再是发散性而是误差的概率区间内涵。
    所以，一个非常遗憾的结论，非专业人士对珠峰高程精度±0.21米的理解是正确的。啊啊，事情是专业人士干的，但非专业人士的解释反而正确，这实在太伤感情了。。。
                                                                          2018 3 24