主题：【原创】GB/T 22554-2010校准曲线线性检验方法简介及Excel计算表

GB/T 22554-2010校准曲线线性检验方法简介及Excel计算表

      化学分析工作经常做校准曲线绘制，然后用回归方程计算校准函数y=a+bx。通常我们习惯用相关系数r是否接近1去评判校准函数的好坏，但是相关系数有一个明显的缺点，即它接近于1的程度与数据组数n相关，数据组n越小越容易得到1，数据组n越大相关系数越容易偏小，这容易给人一种假象。而且相关系数只能说明数据点是否近似在一条直线上（线性关系），不能评估校准函正确度（精密度与准确度）的大小，因此只用相关系数去评价校准函数的好坏是有所欠缺的。

      本帖介绍采用《GB/T 22554-2010 基于标准样品的线性校准》进行校准曲线线性检验的方法，由于GB/T 22554标准中有大量计算，我根据标准制作一个Excel计算表，以GB/T 22554例题的计算过程讲解Excel计算表的用法。为了方便新手入门了解，对于标准中那些让人望而生畏的术语及公式符号，我尽量翻译成直白的话简单说明。当然，如果大家觉得本帖又枯燥又长，也可以从这里开始猛往下滑，只看第三部分Excel表使用说明，也不影响使用本Excel计算表。


    第一部分 首先介绍基于GB/T 22554-2010进行线性校准的标准依据

      《GB/T 22554-2010 基于标准样品的线性校准》
      《GB/T 35655-2017 化学分析方法验证确认和内部质量控制实施指南 色谱分析》
      《GB 17378.2-2007 海洋监测规范 第2部分：数据处理与分析质量控制》

      第二部分  GB/T 22554-2010进行校准函曲线线性检验的方法


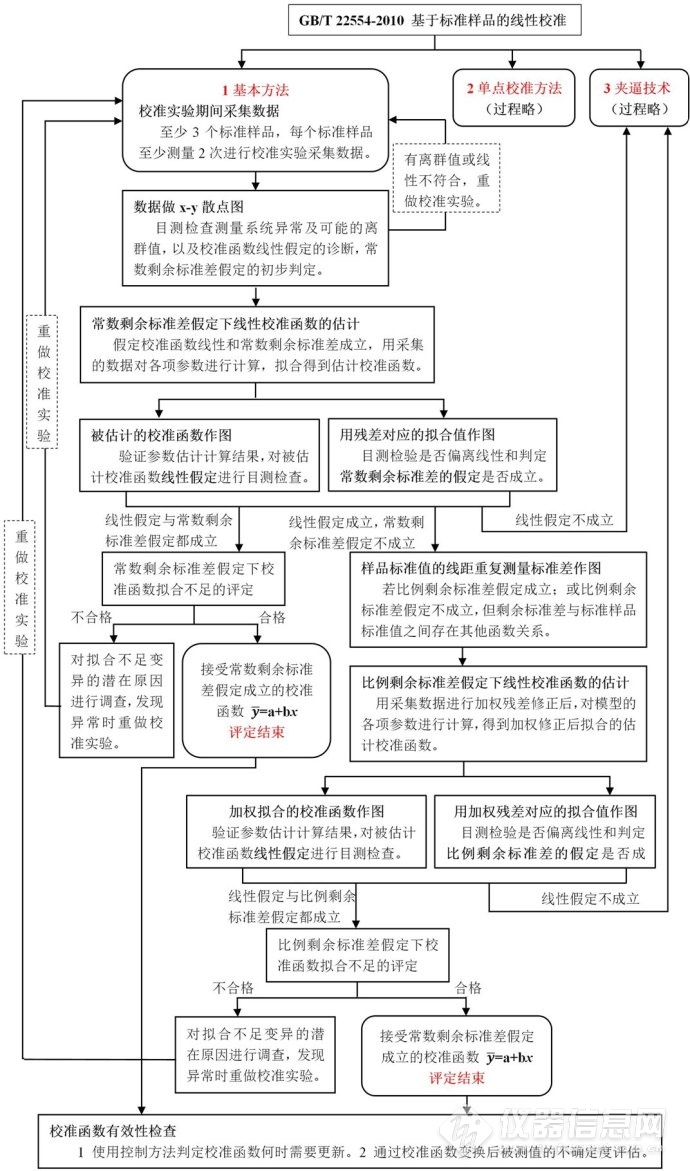
      GB/T 22554-2010校准函数线性检验的步骤，可归纳为以下流程图1：

                       

                                                                        图1 GB/T 22554-201线性校准流程图

      由以上流程图，GB/T 22554线性校准的方法有3个，分别为“基本方法”，以及该基本方法的两种替代方法“单点校准方法”、“夹逼技术”。其中单点校准方法是一种快捷技术，在保证校准函数线性性前提下，只用一个标准样品去“重新校准”测量系统。夹逼技术就是用两个含量尽可能从两侧靠近（或夹住）未知量值的标准物质，去校准测量系统。但是这两种方法在使用上都有局限性，以下主要介绍“基本方法”，“基本方法”按流程图可分为以下10个步骤。

      步骤1 校准实验期间采集数据
      使用至少3个标准样品，每个标准样品至少测量2次进行校准实验采集数据。


      步骤1 校准实验期间采集数据
      使用至少3个标准样品，每个标准样品至少测量2次进行校准实验采集数据。


      步骤2 数据做x-y散点图

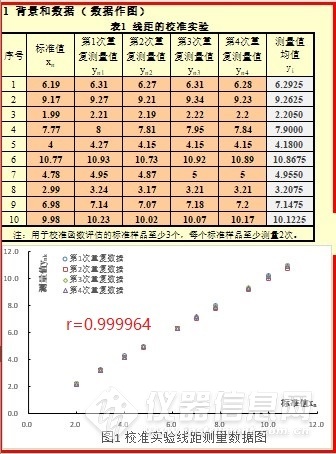
      根据步骤1的数据作图，在这一步骤的作用是目测检查测量系统异常及可能的离群值，以及校准函数线性假定的诊断，常数剩余标准差假定的初步判定。在这个步骤里面如果发现有系统异常和离群值，就要补做数据点或重新试验。见下图2：

                                                     

                                                                              图2 数据采集及作图

      在这一步骤校准函数线性假定的诊断，可以通过相关系数来判断，以上数据计算的相关系数为Rxy=0.999964。要是以前我们一看这相关系数好大，这条曲线好直啊马上就通过了是不是？但是且慢，正如以上说的，这条曲线很直但并不代表这条曲线的精密度也是好的，因此我们还要进行校准函数精密度的评估。

      步骤3 常数剩余标准差假定下线性校准函数的估计
      步骤3的“常数剩余标准差假定”代表两层含义，一是假设校准函数的线性合格（也就是这条曲线很直），另一个是假设“常数剩余标准差”也合格。“常数剩余标准差”我们可以这么简单理解：“剩余标准差”是表征这条曲线上，所有数据点测量值与这条曲线拟合值之间差值（残差）的离散程度。如果一条曲线上所有数据点的残差，都是随机均匀的正态分布状态，那么所有数据点估计出来的“剩余标准差”，就无限接近一个常数（就是某个正态分布密度函数数值），这就是所谓的“常数剩余标准差”。


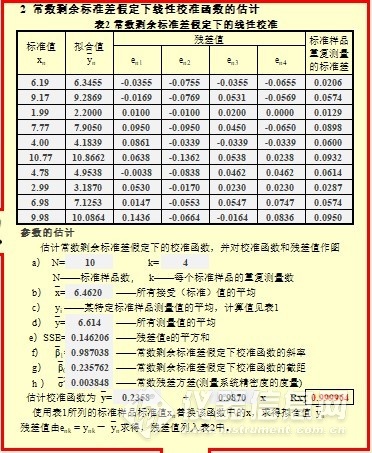
      实际实验操作中，由于仪器、试剂、环境、操作方法等误差因素，往往会偏离“常数剩余标准差”这种理想状态的。在不知道这条曲线精密度的情况下，我们先假设这条曲线是符合“常数剩余标准差”这种理想状态，然后进行各种参数的计算，见下图3

                                                             

                                                                      图3 常数剩余标准差假定下线性校准函数的估计

      步骤4 常数剩余标准差假定下校准函数与残差作图（重点步骤）
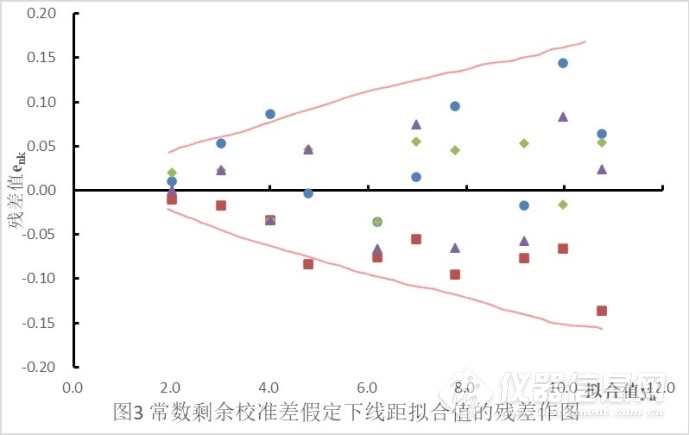
      根据以上步骤3计算出来的校准函数和残差，做出以下3个图，其中有个图是跟上面散点图是重复的，这里不贴了，主要是看下面这两个图4和图5。本步骤不是由公式计算得到一个数值比对大小进行直观的判断，而是需要人工看图用人脑进行评估，因此要重点详细说明：

                             

                                                                图4 常数剩余校准差假定下线距拟合值的残差作图

      先看以上图4线距拟合值的残差图（本帖图片编号与计算表中不同），如果校准函数是符合“线性假定”和“常数剩余标准差假定”这种理想状态的话，那么以上残差图的每一个点应该随机分布在以“0”为中心线的两边，呈正态分布。这样我们就直接跳过以下步骤5、步骤6做“常数剩余标准差假定”的校准函数拟合不足评定，拟合不足评估又通过的话，就可以使用计算的校准函数y=a+bx了。实际上我们平常只要相关系数通过了，就直接得出校准函数y=a+bx的做法，就是这种“常数剩余标准差假定”的缩减版。
      大部分还是出现以下两个情况：
      1） 每个拟合值的点都偏向在中心线的一边，而且每相邻的点都连着一起增大或减小（参见GB/T 22554的图3），这种情况说明校准曲线的这条直线还是不够直，这就要跳出“基本方法”的步骤，采用“夹逼技术”进行评估, “夹逼技术”本帖不详细介绍了。


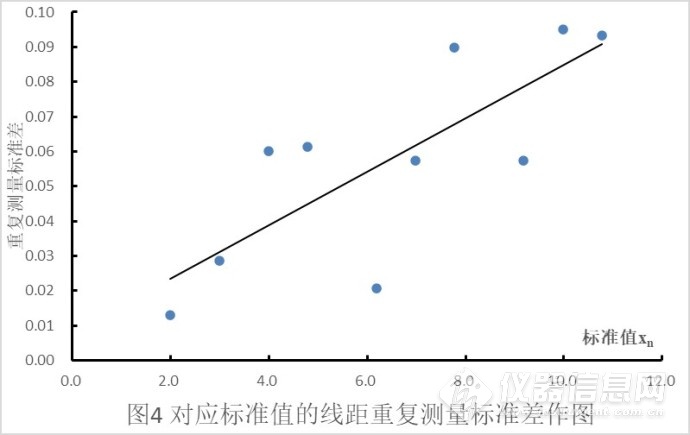
      2） 残差值的散布随着拟合值而增大或缩小，就比如以上图4，拟合值越大，数据点残差的分散就越扩大，就表明偏离“常数剩余标准差假定”了。象这种情况我们再结合图5，进一步判定这条曲线是不是符合“比例剩余标准差假定”。

                               


                                                                      图5 对应标准值的线距重复测量标准差作图

      3）在图5中，如果随着标准样品的标准值的增大，重复测量标准差也跟着增大或减小，这组数据的拟合线也会倾斜着上升或是下降。这就说明了变量“重复测量标准差”的变化总是伴随着另一个变量“标准值”的变化，则两个变量是成比例关系的，也就是所谓的“比例剩余标准差”。
在本例的图5中，这条拟合线是斜着往上升，说明这条曲线符合“比例剩余标准差”，那以下就按“比例剩余标准差假定”的步骤做了。如果这条曲线是符合“常数剩余标准差假定”，则拟合线应该是接近平行线的才对。


    2012年到2014年间楼主实验室还有用分光光度法的时候，也曾用GB/T 22554校准方法Excel计算表进行不少验证，其中一个经验就是：基本上所有曲线校准都是符合“比例剩余标准差假定”，没见过“常数剩余标准差假定”的。

      步骤5 比例剩余标准差假定下校准函数的估计


      本步骤5也是采用步骤1校准实验期间采集的原始数据，重新进行估算。前面常数剩余标准差假定下校准函数模型，不就是因为各个数据点的残差随着拟合值的增大而增大，大小不一样不成立吗？那这个比例剩余标准差假定下校准函数估计的模型，就用倒数关系加权修正，把大的残差变小，把小的残差变大，让所有残差都变成差不多大小，然后对原始数据也加权修正，算出一大堆加权拟合后的参数。这部分的计算步骤跟以上步骤4差不多，这里就不贴图了，具体看Excel计算表。

      步骤6 比例剩余标准差假定下校准函数和残差作图


      接以上步骤5计算的各种参数作图，这里一共是作两个图。其中一个“比例剩余标准差假定下校准函数和残差作图”，也是检验加权拟合后校准函数的线性（看曲线直不值），这里也不贴图了。最主要的还是看图6：

                               
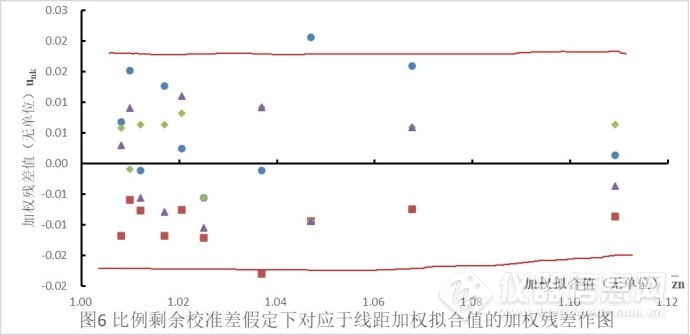
                                                                  图6 比例剩余校准差假定下对应于线距加权拟合值的加权残差作图

      以上图6可以跟以上图4对比，拟合值和残差经过加权修正后，加权残差数值随机散布在以“0”为中心线两边，不再像图4一样逐渐扩大了，这说明加权拟合是成功的，那就接着往下做。

      步骤7 比例剩余标准差假定下校准函数拟合不足的评定


      到这一步骤就是前面提到的校准函数精密度评估了。这个“校准函数拟合不足的评定”的主要内容是用的F显著性检验（ANOVA方差分析），比较前面“比例剩余标准差假定”模型“把大的残差变小，把小的残差变大”加权修正做法所造成的误差，是否大于各个点残差离散分布的大小程度（纯误差）。如果不大于，就说明我们前面的做法是对的，拟合不足评估通过，就可以接受使用计算的校准函数y=a+bx了。具体的计算看下图7：

                                 
                                                                      图7 比例剩余标准差假定下校准函数拟合不足的评定

      表中各种骚操作计算大家可以不用理会，直接看Excel自动判定校准函数拟合不足的线性假定结果成立不成立就可以了。如果还是不成立的话，那就要进行原因调查了，标准中给出不成立的原因是：这条曲线还是不够直，或是没有进行真实的重复性实验。所以说啊，不管相关系数看起来是多么漂亮，曲线图上直线看起来是多么的直，还是到这一步校准函数拟合不足的评定结果说了算。


      而计算表也显示，按我们以往的做法只用相关系数评定，直接得出的校准函数是y=0.2358+0.9870，而用GB/T 22554方法加权修正后的校准函数是y=0.2469+0.9851，校准函数已经有了改变。而拟合不足评定的总偏差平方和则从前者的316.83猛降到0.04，这精密度提高的不是一点半点。这也进一步说明了，只用相关系数判定校准函数好坏是不够的，用GB/T 22554方法则精细的多，结论可靠的多。

      步骤8 校准直线统计检验（参考）


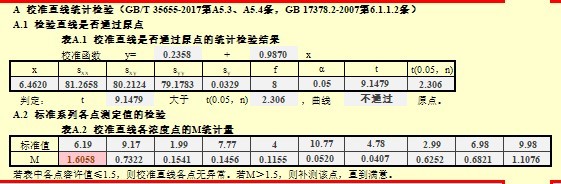
      这一步骤校准直线统计检验不是GB/T 22554的内容，而是参考GB 17378.2的方法，随后GB/T 35655-2017也引用。GB/T 22554修改采用的标准ISO 11096：1996制定年代比较老，因此在GB/T 22554标准里面，检查是否有测量异常值或是测量系统异常的方法，就是看曲线图用目测检查，这就很让人挠头了。而GB/T 35655-2017第A5.3、A5.4条的做法，就是用统计学方法检验直线是否通过原点，及校准直线各浓度点的M统计量这两个项目进行辅助检查，这就比用目测检查的方法可靠多了。以没有修正之前的原始数据做检查为例，得到以下结果：

                                   

                                                                                    图8 校准直线统计检验
      由以上结果得知：
      1）校准函数的截距过大，校准曲线没有通过原点。
      2）标准值为6.19的数据点显示为异常值，这就表明要么是相关系数低于规定值，或是这个浓度点偏离曲线比较大。我们前面算过相关系数是Rxy=0.999964，显然这造成异常值的是后一种原因。我们可也以从上面图4也可以看到，标准值为6.19的4个重复测量值的残差都全部在以“0”为中心线的一边，而且偏离距离超出要求了。这异常值偏离曲线较大，在的曲线图肉眼是看不出来的，这也说明用统计学方法检查的好处。
      如果要查找以上两个原因，以分光光度法为例，可以参考“《分光光度法标准曲线回归与应用的磋商》中国环境监测 1991年 作者：陈禹方”给出的影响因素：
      1）单色光纯度不够；
      2）易挥发的溶剂所引起的测定溶液浓度的改变，或是溶质随溶液浓度的变化出现电离、解离或聚合的程度，或与显色剂生成有色物的配位数改变，不符合比尔定律；
      3）比色皿的厚度或光学性能不一样；
      4）显色反应和反应条件的问题；
      5）操作上的原因
      6）干扰物质的影响。
      以上的原因先不说查找的有困难，就是有些影响因素就算找到了也不好整改（比如说单色光纯度不够）。我们再看Excel表中经过比例剩余标准差模型加权修正后的拟合值，则就能通过原点，而且不出现异常值了，这部分计算结果具体看Excel计算表，这里不贴图了。


这也是我以前使用GB/T 22554校准方法的一个心得，在没有使用之前，如果用GB 17378.2-2007检验出截距过大了有异常值了，要整改起来好麻烦，不整改心里总纠结。使用GB/T 22554校准方法后，大部分检验出的截距过大、有异常值都能修正过来，有点小毛病也不用重新校准试验，起码心里就舒服多了。

      步骤9 校准函数有效性检查
      校准函数使用一段时间后，测量系统漂移或变化可能会导致校准函数失效，怎么判定校准函数已经失效需要重新进行曲线绘制？
很多分析方法标准就笼统的讲述几句要用标准样品进行校准曲线确认的要求，但是又没有明确的评价方法步骤。导致有些试验室在评价过程中没有正确应用，比如说用重复性限，而不是用标准样品准确度值的临界差评定（准确度值的临界差计算方法参见GB/T 6379.6-2009第4.2.3条），这样评价校准函数是否失效的结果也是不正确的。


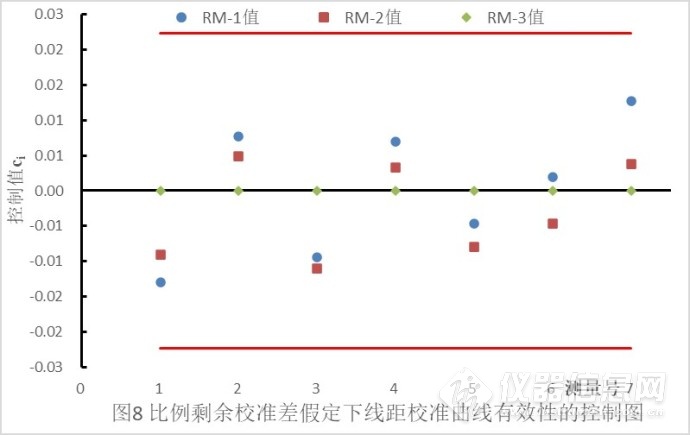
      而GB/T 22554给出一个完整的校准曲线确认的方法和步骤，这个方法使用至少2个尽可能覆盖正常操作条件下含量的标准样品，每个标准样品至少测量2次，定期进行校准曲线确认实验数据采集，计算出上下控制限，并用数据作图评定。以上剩余标准差假定校准函数y=0.2469+0.9851为例，选用最高和最低值含量的标准样品进行校准曲线确认数据采集，计算过程见Excel表，最后作图是这样的（请忽略本帖图号与Excel图号不同）：

                         
                                                                            图9 比例剩余校准差假定下线距校准曲线有效性的控制图
      本图中，对常数剩余标准差模型也好比例剩余标准差模型也好，当一个或多个di落在上下两条控制限的红线之外，则认为系统失控，需重新对m个标准样品进行测量。若重新测量的m个样品中至少有一个值仍落在控制限外，应对该点做调查，查找问题的原因。根据问题的性质，可能需要进行新的校准实验并对校准函数重新估计。以上图9中，经过连续7次检查，每次两个标准样品测量值与真值的误差点，都还在控制限上下限红线内，表示系统处于受控状态，校准函数y=0.2469+0.9851还能继续用。


      从以上计算原理，本方法计算控制值控的控制限，也是起到准确度值临界差的作用，从而评定校准函数的准确度（看看测的准不准）。在有些分析方法标准没有给出精密度（重复性限与再现性限），从而计算实验室测量结果准确度界限的，可以用本方法代替。

      步骤10 校准函数有效期内变换值的不确定度评估


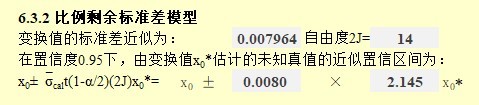
      GB/T 22554还贴心的给出本次校准函数有效性检查合格后，只要是在有效期内平常做试验时，试验样品采用本校准函数计算结果的测量不确定度评定方法，计算过程与结果看Excel计算表与标准，结果控制图见下图：

                                       
                                                                    图10 校准函数有效期内变换值的不确定度评估
      本标准的不确定度评估方法，与其他GUM不确定度评估方法标准相比，本标准方法每次仅用2~3个标准样品，进行2次以上重复性测量。评估时仅通过测量数据计算标准偏差评估不确定度，不像其他GUM标准还要分A类、B类多个分项不确定度评估，而且还能随着后续校准函数有效性检查的补充数据，实时更新不确定度数值，方便是比较方便了。
      按我以前在同等试验条件下，用本不确定度评估方法的结果，比其他GUM方法的评估结果要小一些，但是结果差别又不大到像是没有加入B类不确定度分项的原因。虽然说业内对不确定度评定要不要分A类B类评定还有争议，但我对不确定度评估这方面也是半桶水，不好乱下结论说本不确定评估方法能不能用。而且这种GB/T 22554不确定度评估方法是在太小众，一般试验室评审时，我都是给评审员看用JJF 1059.1-2012、GB/T 27411-2012、GB/T 28898-2012等比较大众方法评定的不确定度报告。
      当然了，对于一些小试验室没有能力评定不确定度的，也可以用本方法先凑合着用。


      第三部分 GB/T 22554-2010Excel计算表使用说明

      本部分总算不讲那些枯燥的东西了，我估计不少人是囫囵吞枣的跳下来看的是不是？不过这真的不要紧的，本GB/T 22554Excel计算表设计为傻瓜式的使用，前面内容看个大概也不影响使用。
    1）GB/T 22554-2010Excel计算表的使用说明（根据跟帖坛友反馈本文内容太多太复杂，因此红色标注提示只看这一条，其他的内容可以忽略也不影响计算表的使用）
      本Excel计算表的使用步骤顺序为：
      a）试验室按步骤1进行校准实验采集数据，输入到Excel表1。
      b）然后按步骤4的要求，看看Excel图3、图4，是符合“常数剩余标准差假定”还是“比例剩余标准差假定”，按楼主我以往的经验，大部分都是按“比例剩余标准差假定”的步骤往下走。
      c）基本上直接跳到步骤7，看Excel表“5.2比例剩余标准差假定下校准函数拟合不足的评定”，如果最后结论结果显示“线性假定成立”，就可以接受并使用校准函数了。如果到这一步发现还是有异常，就说明测量系统出大问题了，这时就结合Excel表第二部分校准直线统计检验的结果，看看是哪个点出异常值还是直线没通过原点，这时就按步骤8进行整改吧。
就这三个步骤一路看下来看结果这么简单，结果有不合格栏目的Excel表自动显示红色，避免遗漏。
    2）GB/T 22554-2010Excel计算表的有效数字位数问题
      由于每种试验方法最终结果的有效数字的位数不一样，如果使用当中需要对校准函数最终结果截距a或是斜率b的有效数字进行位数修约的，可参照我的另外一个帖子《EXCEL采用VB实现指定修约间隔及指定有效数字四舍六入五留双修约方法》自己对Excel进行修改,如有提示启用宏就打开宏：
      https://bbs.instrument.com.cn/topic/7235930。
      但是注意在计算过程中结果的修约位数不要去改动，GB 17378.2-2007第5.1.4条规定“在修约计算过程中对中间结果不必修约，将最终结果修约到预期位数”。按计算机普遍使用情况下，现在好多标准包括GB/T 22554例题的最终结果，也是用某种计算软件中间不修约计算出来的，标准中计算过程结果为了写的好看才修约。如果觉得不好看去改动计算过程中结果的修约位数，就会出现和GB/T 22554最终结果不一样。
      在GB/T 35655-2017也有一个例题，大家有兴趣可以用GB/T 35655的数据进行计算验证，但是GB/T 35655-2017在A.4.3条“比例剩余标准差假定下校准函数的估计”步骤，对原始数据加权修正好像出了点问题，计算出校准函数的截距值“a=-0.0030”，正确的应该是“a=-0.00034”，少了个0后面的一片跟着错下去。还有GB/T 35655-2017第A.5.3条“检验直线是否通过原点”部分，即使是按标准中截距值“a=-0.0030”计算，最后计算的t值也好像是错的哎。



      第四部分 GB/T 22554-2010线性校准方法使用总结

    1）GB/T 22554-2010线性校准方法的特点
      GB/T 22554线性校准方法的特点，是本方法独有的比例剩余标准差校准函数模型，模型中用倒数关系把大的残差变小，把小的残差变大进行加权修正。这种加权修正做法最直观的作用，就是减小校准曲线两端高低含量测量值的方差，则。减小的误差在常量分析中的好处可能不明显，但是在比如色谱分析的微量、半微量分析就比较有优势了，特别是做中实国金能力比对试验，遇到某些元素含量比较刁钻的样品，有时候是真的能救命。
      GB/T 22554标准的线性校准方法，比其他标准的方法或是计算软件自带方法更加全面，基本上校准曲线绘制遇到的问题都能在这里解决。前面也说了不少GB/T 22554线性校准方法的种种好处，也是我极力推荐本标准的理由。
    2）GB/T 22554-2010线性校准方法的使用推广
      GB/T 22554修改采用的ISO 11096：1996标准，至今已有二十多年，ISO标准组织每5年都对ISO 11096标准进行审查，至今仍然有效，说明本标准方法使用多年依然经得起考验。我国在2010年引进本标准为GB/T 22554也有10年，但是这么一个宝藏方法标准，至今在知网、万方、维普等网站都还没有对本标准进行介绍推广的文章，这也说明GB/T 22554在国内的使用率还是不高。
      GB/T 22554难于推广使用，不止是海量的计算，还在于其中某些步骤需要人工手动判定，这使得本方法难于在主流统计计算软件的Minitab、OriginPro、SAS、MATLAB等采用（当然MATLAB可以与python接口或是使用python可以实现人工判定的步骤，不过这不在本文讨论之内），所以大众难于使用本标准方法。幸好我们还有万能的Excel，自己设计一个GB/T 22554Excel计算表，降低使用门槛，让更多的试验室使用本标准，提高本试验室的检测能力水平。
      目前大部分国内外厂家的仪器设备，仪器测量软件内置的线性校准方法，都是很简单的线性校准检验，最多是进行回归方差分析。如果有能力厂家的测量软件使用本标准的线性校准方法，可以为客户提供更精确的校准函数、校准函数合格检查、异常值检查、校准函数有效性检查、甚至是不确定评定等服务项目，这对很多化学分析初学者都是一个福音。

    后续：本文作为科普贴，在标准介绍过程中对有些名词术语的解释不是很正规，甚至是存在错误。正规的解释请参照我的另外一个帖子：合适新手自学数理统计用的书籍与统计软件简介 https://bbs.instrument.com.cn/topic/7355109 。如果有错误的地方请大家指出，我继续修改完善。
      仪器信息网论坛的本数据处理版块，前面已有calfstone和wazcq两位前人对本标准做过介绍，本文也是在两位前人努力的基础上添砖加瓦。特别是有幸看到calfstone的帖子我才知道这个标准，他的帖子有GB/T 22554-2010标准下载：https://bbs.instrument.com.cn/topic/3467111 。其他标准，在网上都有下载，这里就不附上了。
      楼主我学分析化学的，但工作后离化学渐行渐远，时至今日让我配个溶液都困难。这个Excel标准放我这里荒废很久实在可惜，所以分享出来，让更多人继续完善下去，也希望本Excel计算表能为GB/T 22554的推广使用尽到一份力量。