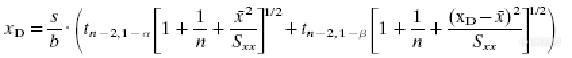![]() 三、检出限的理论核心
三、检出限的理论核心理解检出限的理论核心必须建立在三个重要前提的理解上面:
1、对测量的统计特性的理解上,正如我们所指出的那样,测量总是带有一定的随机误差,这种随机误差决定测量的结果总是一个带有分布的范围,可以用特殊的分布函数来描述。
2、现有的测量基本是相对测量,我们必须先区分仪器响应信号(信号域)和浓度或量(浓度域)的差别。不管是信号域还是浓度域都同样具有统计的特性,我们往往首先得到信号域的结果。
3、统计学上的两类错误。任何判断在统计学上都会犯两类错误。针对判断检出限与空白相比较的例子,如果我们说空白信号/浓度比我们设定的检出限低,这个时候就可能犯I型错误(α);如果我们说我们设定的检出限比空白信号/浓度高,这个时候就可能犯II型错误(β)。IUPAC(95版)在定义检出限的时候用了三个比较抽象的数学公式;
1、临界值Detection decision (critical value) (LC,α=0.05)
![]()
2、检出限Detection limit (minimum detectable value) (LD,β=0.05)
![]()
3、定量限Quantification limit (minimum quantifiable value) (LQ,RSDQ=0.10)
![]()
其中KQ=1/ RSDQ=10
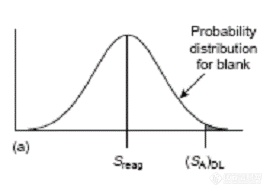
要理解以上抽象的数学公式可以用图1,2加以说明(其中I型错误和II型错误分别用黑色和灰色表示):
![]()
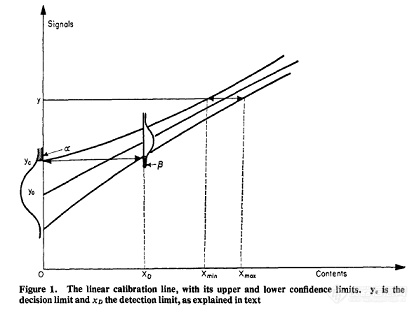
![]() 图1 临界值的示意图对于空白测定的结果可以用图1中a表示,我们首先的目的是找到比空白大的一个临界值(SA)DL,显然空白的大部分都比临界值(SA)DL比小,但实际还是有黑色的小部分比我们划定的临界值要大,这就是I型错误。早期Kaiser就是用此临界值作为方法检出限,但此时II型错误高达50%(见图1中b)。后来,Currie完善了检出限的统计完备性,采用α=β=0.05来规定检出限,这时候我们可以用图2来表示。即规定α=β=0.05错误概率,我们对于检出限的理解依然还是定性的检出。要想准确定量样品中的浓度,必须还要减小错误概率,定量限采用限定RSDQ为0.10方法,此时的错误概率远远小于0.05。
图1 临界值的示意图对于空白测定的结果可以用图1中a表示,我们首先的目的是找到比空白大的一个临界值(SA)DL,显然空白的大部分都比临界值(SA)DL比小,但实际还是有黑色的小部分比我们划定的临界值要大,这就是I型错误。早期Kaiser就是用此临界值作为方法检出限,但此时II型错误高达50%(见图1中b)。后来,Currie完善了检出限的统计完备性,采用α=β=0.05来规定检出限,这时候我们可以用图2来表示。即规定α=β=0.05错误概率,我们对于检出限的理解依然还是定性的检出。要想准确定量样品中的浓度,必须还要减小错误概率,定量限采用限定RSDQ为0.10方法,此时的错误概率远远小于0.05。![]()
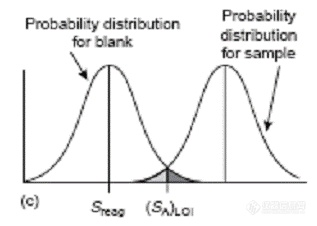
图2 检出限示意图统一检出限的相关概念,完善检出限的统计完备性都是相对比较容易的事情。现有检出限的争论,分歧主要在于以下几个方面的问题:
1、空白。空白的定义本身就有很大的歧义,采用什么样的空白来评价检出限必然带来检出限的差异,例如《全球环境监测系统水监测操作指南》采用零浓度样品来定义空白,也有用试剂空白的,还有用加标的空白样品的。理论上讲,最好的空白是零浓度样品,但实际工作很少能找到这样的东西。还有更为郁闷的情况,空白进入仪器后只显示0,这样的话你就没办法评价空白的标准偏差,更无法计算检出限了。
2、分布的正态假设和置信概率的随意性。现有的检出限理论都采用正态近似的假设,但实际测定中空白的分布不一定满足正态。不同的人对置信概率把握不同,必然带来同一实验不同的检出限结果。
3、从信号域到浓度域推算。由于我们得到的多数是信号域的空白分布特性,如何从信号域换算浓度域的检出限也是争论很多的问题。是采用标准曲线推算灵敏度呢?标准曲线又该如何设置呢?还是用较低浓度的CRM来做单点校正?
![]()




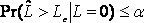
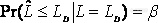
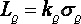 其中KQ=1/ RSDQ=10
其中KQ=1/ RSDQ=10