Acid Content:
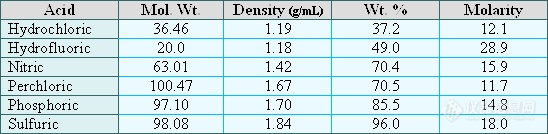
Another area of confusion is the expression of the acid content of the solution. We all agree that it is important to matrix match the standard and sample solutions to avoid a fixed error in the solution uptake rate and/or nebulization efficiency sometimes referred to as a matrix interference. If a solution is labeled as 5% HNO3 what does this mean? If we take 5 mL of 70% concentrated nitric acid and dilute to a volume of 100 mL then this is 5% HNO3 (v/v) where the use of 70% concentrated acid is assumed. However, nitric acid can be purchased as 40%, 65%, 70%, and > 90%. Therefore, note the concentration of the concentrated acid used if different from the 'norm' as well as the method of preparation i.e. v/v or wt/wt or wt/v or v/wt. The wt. % concentrations of the common mineral acids, densities, and other information are shown in the following table:
Table 3.3: Wt. % Concentrations
![]()
Acid Content in Molarity:
It is important to know what the concentration units of the concentrated acid being used mean. Taking 70% concentrated nitric acid as an example means that 100 grams of this acid contains 70 grams of HNO3. The concentration is expressed at 70% wt./wt. or 70 wt. % HNO3. Some analysts prefer to work in matrix acid concentrations units of Molarity (moles/liter). To calculate the Molarity of 70 wt. % nitric acid we calculate how many moles of HNO3 are present in 1 liter of acid. Lets say that we tare a 1 liter volumetric flask and then dilute to the mark with 70.4 wt. % HNO3. We would then measure the weight of the solution to be 1420 grams. Knowing that the solution is 70.4 wt % would then allow us to calculate the number of grams of HNO3 which would be (0.704)(1420g) = 999.7 grams HNO3 per liter. Dividing the grams HNO3 by the molecular weight of HNO3 (63.01 g/mole) gives the moles HNO3 / L or Molarity which is 15.9 M. The above logic explains the following equation used for calculating the Molarity of acids where the concentration of the acid is given in wt %:
[(% x d) / MW] x 10 = Molarity
Where:
% = wt. % of the acid
d = density of acid (specific gravity can be used if density not available)
MW = molecular weight of acid
Using the above equation to calculate the Molarity of the 70 wt % nitric acid we have:
[(70.4 x 1.42) / 63.01] x 10 = 15.9 M
Dilutions of the concentrated acid to prepare specific volumes of specified Molarity can be make using the (mLA)(CA) = (mLB)(CB) equation.
Avoiding Precipitates:
In the preparation of mixtures of the elements, it is good to avoid the formation of precipitates. It is common to form precipitates when concentrates of elements that are considered compatible (see part 1 of this series) are mixed. Many precipitates are not reversible (i.e., will not go into solution upon dilution). It is therefore best to add all of the acid and most of the water to the volumetric flask or standard solution container (dilutions to weight) before adding the individual element concentrate aliquots. Mixing after each aliquot addition is strongly advised. When diluting to volume it is often found that the solution is above room temperature. Therefore allow the solution to cool to room temperature and adjust to the mark with DI water. It is best to prepare the dilution the day before needed to allow for proper volume adjustment.
Storage
The following are some considerations you may want to make before the storage of chemical standard solutions:
Know the chemical stability of your standard. Chemical stability can be altered by changes in starting materials and preparation conditions. It is therefore advisable to perform stability studies on all standard solutions to avoid time consuming and costly delays or mistakes and to strictly adhere to preparation methodology, including order of addition for multi-component standard solutions.
Note the temperature during storage and attempt to maintain a storage temperature at or around 20 °C. Some standards are not stable for long periods at room temperature and require refrigeration or even freezing.
Perform the stability study in the container material selected for storage. It is not advisable to use volumetric flasks as storage containers due to expense, contamination, and transpiration issues.
Determine if the standard is photosensitive and/or store in the dark if there is a concern. This is an issue with some of the precious metals and is a function of matrix. Photosensitivity will increase in the presence of higher energy light (sunlight as opposed to artificial light) and trace or minor amounts of organics especially if there is an extractable proton alpha to an electron withdrawing functional group such as a carbonyl group. The presence of chloride may increase instability to photo reduction. A classic example is Ag+ in HCl solutions.
Store the standard in containers that will not contribute to contamination of the standard. LDPE is an excellent container for most inorganic standards.
Weigh the standard solution before storage and then just before the next use. If there is measurable transpiration the weight will decrease with time