主题：【原创】直读测定铝合金中的铬

首先说明的是，您对曲线下限的观察很细致，我们所说的曲线，实际上是代表强度比与含量之间的函数关系，我们常用的二次、三次函数关系只是在一定范围内“近似为真”。真实的光强和含量之间的关系形式应该是赛伯-罗马金公式的形式： lgI=lga+blgC。因此，对于“一定范围内”的这个范围，我们要有一个比较清楚的认识。首先，根据常识我们应该可知，无论这个函数关系式怎样的，他都应该是单调增的，即含量越高，光强越大，反之亦然。因此，在采用二次，三次函数关系时，首先要看做出的函数关系在我们的整个测量范围内是否呈一个单调增的态势。第二，实际的含量与光强均不可能为负，因此横纵坐标都没有副半轴。由于背景光、光谱干扰以及暗电流的影响，在实际元素含量为0时，该通道测量到的光强通常不能完全达到0。因此，有几种情况可能会造成“负含量”的计算结果。
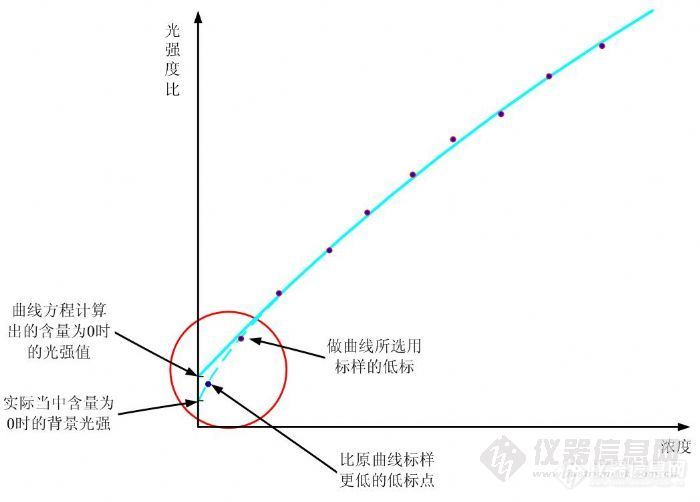
1、曲线低标含量比测量样品含量高，因此在曲线在此低含量区域内的拟合效果与实际变化规律并不“近似”，而在低标与高标范围内的测量是近似于真实的，因此对于此含量范围内的样品，测量结果基本不受影响。这种情况可以通过加入含量更低的低标样品参与拟合来解决，如下图所示：
2、制作曲线时，背景光强不稳定，或光谱干扰扣除错误造成的。详细说来是当背景光强远大于真实信号光强时，细微的背景光跳动会淹没实际元素在痕量范围内的变化，如果做曲线时，背景光强测量值偏大，则在实际测量中，当元素含量低时，会计算出负值。出现光谱干扰扣除错误时亦是同理。这种情况可以有几种解决办法，首先对于光谱干扰，找到正确的干扰元素与合适的校正系数，校正算法是关键。如果条件限制不能实现，那么恰当的选用含量适合的控样（类标）也是可行的办法。对于背景不稳定的情况，适当的调整激发状态，适量降低曝光时的峰值电流，增长曝光时间或增大曝光频率等等，有时可以起到不错的效果。

看了半天的文字不如一张图来的直接，你实验室不做方法不确定度评估吗？

没做，您是否可以介绍一下这个直读光谱的不确定度评估的方法步骤？谢谢。

GB/T 6379的6个分册，，，写的比较麻烦，没全看明白呢还，，，你可以自己看看吧

专家讲的很详细，我记得我们以前是元素干扰问题，不知道你们最终是什么原因啊，你用什么仪器

大部分是元素干扰。

还是先从样品材质找找看。。