一. 数学模型∶![]()
式中:
w∶待测样品中目标组分的含量,ug/g;
C0: 提取液中目标组分的含量,ug/ml;
V0: 提取液的体积,ml;
m: 待测样品的称量量,g 。
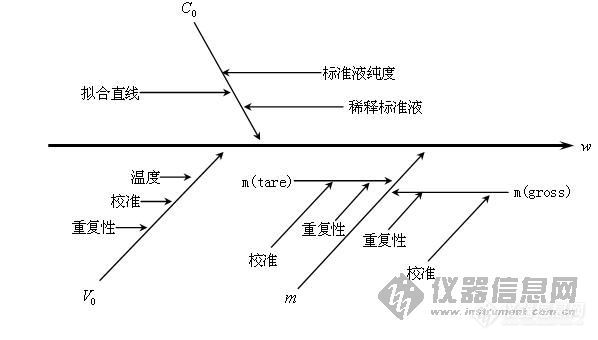
二.因果图∶![]() 三 计算各分量标准不确定度∶
三 计算各分量标准不确定度∶3.1 V0 的不确定度
该体积有三个主要的影响:校准、重复性和温度影响。
①校准:制造商提供的容量瓶在20℃的体积为25ml±0.03ml,给出的不确定度的数值
没有置信水平货分布情况,因此假设是必要的。在这里,计算标准不确定度时假设为三
角形分布。
![]()
注:选择三角形分布是因为在一个有效的生产过程中标定值比极限值可能性更高。最
终分布用三角形分布比矩形分布表示更好。
②重复性:由于充满容量瓶的变化引起的不确定度可通过该容量瓶的典型样品的重复性
实验来评估。对典型的25ml容量瓶充满10次并称量的实验,得出标准偏差为0.01ml。
这可直接用作标准不确定度。
③温度∶根据制造商提供的信息,该容量瓶已在20℃校准,实验室的温度在±5℃之间
变动。该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计算。液体
的体积膨胀明显大于容量瓶的体积膨胀,因此只需考虑前者即可。丙酮的体积膨胀系数
为0.00149℃-1 ,因此产生的体积变化为±(25×5×0.00149)= ±0.19ml。
计算标准不确定度时假设温度变化是矩形分布,即
![]()
合成三种分量得到V0的相对标准不确定度
![]()
=
![]()
=0.0040。
3.2 m 的不确定度:
相关称量信息:
容器和待测物:0.8836g (观测)
容器和减量的待测物:0.6984g (观测)
m:0.1852g (计算)
根据经验得知,以上两个观测值重复性的标准偏差为0.0001g。
校准∶由天平的校准证书得知,天平的扩展不确定度U=0.00039g(p=95%,k=2.0),所以天平的标准不确定度u=U/2≈0.0002g。
上述两个分量必须各计算两次。由此得到m 的标准不确定度
![]()
m 的相对标准不确定度=
![]() 3.3 C0 的不确定度∶
3.3 C0 的不确定度∶CO的不确定度由三个部分构成∶当由五种标准溶液的浓度-响应面积的直线求得时测量所产生的不确定度、由标准贮备液配制成五种浓度标准溶液时所产生对 的测量带来的不确定度以及标准贮备液自身的不确定度。
①五种标准溶液的浓度-响应面积直线求得 时测量所产生的不确定度。
![]()
上表是五种标准溶液的浓度-响应面积的数据。拟合的直线方程为∶
A = 36572.37 C + 8011.1
记B1=36572.37,B0=8011.1
其中 C=溶液浓度
A=溶液的响应面积
B1=直线斜率
B0=直线截矩
对C0进行2次GC/MS测试,由响应面积通过直线方程求得C0=0.73509mg•L-1,则
C0的标准不确定度为∶
![]()
式中B1=36572.37
![]()
=340.24241
P = 2 (对C0进行2次GC/MS测试)
n = 5 (对每个浓度标液进行1次测量共1×5=5次)
![]()
=0.5016
![]()
=0.2795584
将数值带入
![]()
=0.0088014mg•L-1
![]()
=
![]()
=0.012
②由标准贮备液配制成五种浓度标准溶液时所产生对 的测量带来的不确定度。
C1=0.1672 mg•L-1标准溶液,是将贮备液(83.6 mg•L-1,U=6%,k=2)按1:50,
然后1:10分两次稀释到0.1672 mg•L-1。(标准液溶剂为甲苯,稀释用溶剂为丙酮)
这里1:50稀释是采用1ml移液管和50ml容量瓶来完成的;1:10是采用1ml
移液管和10ml容量瓶来完成的。
不确定度主要有∶校准、重复性和温度影响。
校准∶移液管(A级)在20℃的给出的体积为1±0.007ml,按三角形分布计算,
![]()
=0.0029ml
A级容量瓶在20℃的给出的体积为50±0.05ml,按三角形分布计算,
![]()
=0.020ml
10mlA级容量瓶在20℃的给出的体积为10±0.02ml, 按三角形分布
![]()
0.0082ml
重复性∶对典型的1ml移液管充满10次并称量的实验,得出标准偏差为0.001ml;对典型的50ml容量瓶充满10次并称量的实验,得出
标准偏差为0.015ml; 对典型的10ml容量瓶充满10次并称量的实验,得出标准偏差为0.008ml。这可直接用作标准不确定度。
温度∶容量瓶和移液管已在20℃校准,实验室的温度在±5℃之间变动。该影响引起的不确定度可通过估算该温度范围和体积膨胀系数来进行计
算。液体的体积膨胀明显大于容量瓶的体积膨胀,因此只需考虑前者即可。甲苯的体积膨胀系数为0.00109℃-1 ,因此移液管移取1ml甲
苯产生的体积变化为±(1×5×0.00109)= ±0.00545ml。丙酮的体积膨胀系数为0.00149℃-1 ,因此移液管移取1ml丙酮产生的体积变化为
±(1×5×0.00149)= ±0.00745ml,50ml容量瓶产生体积变化为±(50×5×0.00149)= ±0.3725ml。10ml容量瓶产生的体积变化为±(10×5×0.00149)= ±0.0745ml。
合成以上三项,稀释标准液C1时产生的相对标准不确定度
![]()
=
![]()
=0.0147
经计算,
![]()
=0.0146
![]()
=0.0166
![]()
=0.0165
![]()
=0.0144
合成以上五个分量,由标准贮备液配制成五种浓度标准溶液时所产生对C0的
测量带来的相对不确定度=
![]()
=0.034
③标准液本身的不确定度。
根据标准液证书给出的相对扩展不确定度为6%(p=95%,k=2),计算得出其相对标
准不确定度=6%÷2=3%。由于标准液被稀释成五个浓度,所以标准液的稀释成5个浓
度带来的相对标准不确定度= =0.067。
合成①②③步骤得到 的相对标准不确定度为
![]()
=0.076
所以
![]()
=
![]()
= 0.076
![]()
=
![]()
=99ug/g
![]()
=99×0.076≈8 ug/g

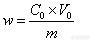
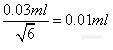
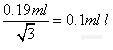
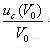 =
= 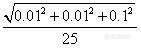 =0.0040。
=0.0040。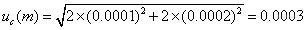
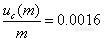

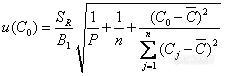
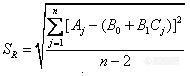 =340.24241
=340.24241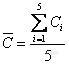 =0.5016
=0.5016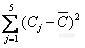 =0.2795584
=0.2795584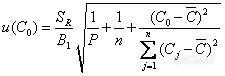 =0.0088014mg•L-1
=0.0088014mg•L-1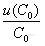 =
=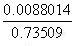 =0.012
=0.012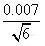 =0.0029ml
=0.0029ml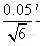 =0.020ml
=0.020ml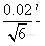 0.0082ml
0.0082ml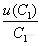 =
=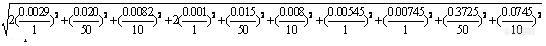 =0.0147
=0.0147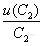 =0.0146
=0.0146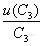 =0.0166
=0.0166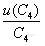 =0.0165
=0.0165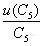 =0.0144
=0.0144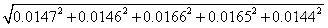 =0.034
=0.034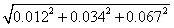 =0.076
=0.076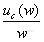 =
= = 0.076
= 0.076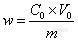 =
=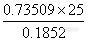 =99ug/g
=99ug/g =99×0.076≈8 ug/g
=99×0.076≈8 ug/g