粒度分布数据量较多,不能一目了然。为了简明,需用一些能代表样品粒度某些特征的参数来描述其粒度情况,这些参数就叫特征粒径。
平均粒径是特征粒径中的一个分支。
D(4,3)体积(重量)平均直径.在D(4,3)的计算公式里4和3是两个常数,表示粒径对体积(重量)的加权平均,称为体积平均粒径或重量平均粒径。
D(1,0)表示粒径对颗粒个数的加权平均,称为颗粒数平均粒径。
on
D(3,2)表面积平粒径,又称为索太尔(Sauter)平均粒径。
D(1,0)使用领域极小,且最流行的激光粒度仪基本不会提供此参数,接触的人少。
除非颗粒是单分布(即所有颗粒都一样大),否则D(3,2)永远比D(4,3)小。
粒径分布的离散度越大,它们的差别就越大。
两个样品的D(4,3)接近而D(3,2)差别大说明了,D(3,2)小的那个样品的粒径分布离散度大于另一个样品。通俗的话说就是一个样品粒度分布较宽,一个样品相对分布较窄,这是本质。
至于比表面积的大小等问题属于表象,一般来讲当D(4,3)接近时, D(3,2)小的那个样品(也就是宽分布样品)比表面积会大一点(前提假设是颗粒都是实心球体的情况下,否则根本不能依据粒度来比较比表面积)。但是这种说法不是绝对的,多峰分布样品也许就不能这样说了,我也没有专门研究过
D(4,3)与D(3,2)的差距在任何情况下都跟颗粒圆度完全不相关。圆度是个颗粒形貌问题,跟粒度分布一点关系也没有,但是颗粒图像处理仪这种粒度仪能够分析颗粒圆度。
附件中的WORD文档是平均粒径的数学定义公式,供大家参考
![]()
![]() 数学定义公式
数学定义公式



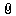 数学定义公式
数学定义公式