然而在实际过程中,系综的旋进过程并非完全“自由”,主要表现在下面两点:
1、密度矩阵的populations并非一成不变,而是随着时间推移慢慢向平衡位置移动
2、密度矩阵的相干项同样会随着时间推移而逐渐减小为0
这一现象产生其实是较容易理解的。虽然我们是以系综的观点来讨论自旋体系,但是实际情况下自旋核之间不可避免会相互影响,如果我们以某一自旋核作为观察对象,周围核自旋所产生的微观磁场无时不刻不在发生着变化,这一磁场与外磁场的矢量和才是这一核真正的旋进轴及旋进频率。虽然这点变化与外磁场相比是微不足道的,但是由于原子核的Larmor频率非常大(如400 MHZ核磁下质子在1秒钟内要完成约4x108次的旋进),每一次旋进轴及频率的改变都将对自旋核的旋进过程产生微扰,正是许多次微扰的累加使得原子核最终趋向于能量较低的自旋取向。而经历了脉冲激发后的原子核毕竟处在一个能量较高的状态,随着脉冲的消失以及时间的流逝,旋进微扰将最终导致原子核回到最初能量最低的平衡状态。其中1为与纵向磁化矢量相关的T1弛豫;2为与横向磁化矢量相关的T2弛豫。
T2弛豫作用于密度矩阵中的相干项,由于这一弛豫最终造成的是相干项以指数形式趋向于0,定义T2为T2弛豫时间,我们取λ=1/T2,则之前自由旋进下的密度矩阵相干项修正为
![]()
同样,考虑了T1弛豫后的密度矩阵populations项的方程修正为
![]()
其中
![]()
最终,在考虑了T1,T2弛豫作用之后,(π/2)x脉冲作用下的密度矩阵变化如下
![]()
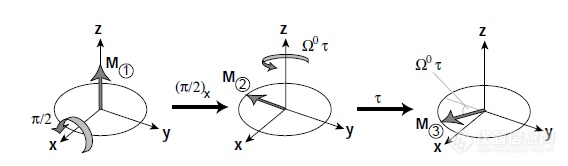
这表明真实的旋转坐标系下的自旋体系旋进过程为下图所描述的过程
![]()





 ;
;





 其中
其中

