主题：讨论关于球差校正电镜和普通电镜CTF曲线的比较

原文由 iamikaruk(iamikaruk) 发表:
高分辨不是完全的phase contrast，它里面包含有amplitude contrast的信息。以前只讨论CTF的虚部是因为以前一直认为高分辨下的样品满足weak phase object approximation，所以实部忽略不计，而且定性来说解释的比较好。而现在则发现weak phase object approx.很难满足，即使是4nm的样品它也不满足这个近似，所以单纯考虑CTF的虚部是不行的，还要考虑其实部。另外这是在线性成像框架下讨论的结果，实际上还要考虑非线性成像，这个影响更大。

原文由 turkeyzz(turkeyzz) 发表:
高分辨里面包含有amplitude contrast的信息这个不错，现在只是考虑由于在样品很很薄的情况，虚部对衬度起决定作。但为什么在只考虑样品很薄的情况下，CTF函数中却没有一段较宽的平坦区域处于-1附近，这不就是说高分辨像不能很好的反应晶体式样的投影结构？我原本的意思是这个哦

原文由 iamikaruk(iamikaruk) 发表:
高分辨不是完全的phase contrast，它里面包含有amplitude contrast的信息。以前只讨论CTF的虚部是因为以前一直认为高分辨下的样品满足weak phase object approximation，所以实部忽略不计，而且定性来说解释的比较好。而现在则发现weak phase object approx.很难满足，即使是4nm的样品它也不满足这个近似，所以单纯考虑CTF的虚部是不行的，还要考虑其实部。另外这是在线性成像框架下讨论的结果，实际上还要考虑非线性成像，这个影响更大。

原文由 蓝莓口香糖(drizzlemiao) 发表:
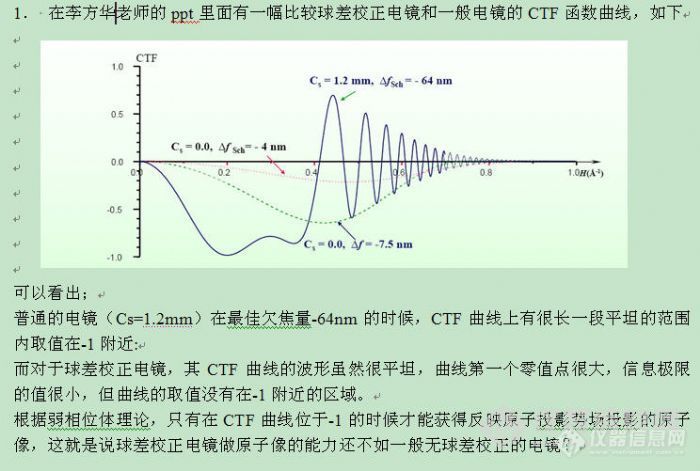
现在就先只说虚部的问题吧。虽然球差可以校正到0，但是高阶像差会继续出现，所有像差的总和是个空间频率的多项式，里面每个项的幂次不同。像差的影响是使电子波相位发生移动，所以这个多项式的值就决定了相位移动的多少。弱相位体近似下，衬度传递函数是取了像差函数的正弦。如果相位移动达到±π/2，传递函数就能取值±1。但是那个多项式随空间频率的变化是比较复杂的，在一定的范围内，虽然出现起伏，但不一定能达到±π/2，由此得到的传递函数的值自然就不是1。
我随便找了两张图，大概能解释这个意思。

原文由 longwood(templus) 发表:
关键是绝大部分样品都不是相位体。

如果是相位体，平面波入射，物体下表面出射波只有位相的改变，没有振幅的改变，那么球差校正的显微镜还不如有球差的显微镜。因为球差校正的显微镜，虽然能将物体出射波完整的传递到像平面，但是我们所能记录的只有电子的强度或者振幅，如果只有位相的变化，在正焦的情况下，我们是看不到任何衬度的，也就是得不到任何结构信息。相反有球差的显微镜，通过球差的作用能形成一定的幅度衬度，反而能被观察到。

所以，就我所理解的HRTEM是phase contrast，不是指出射波只有位相的变化，而是指出射波由于样品的多束衍射的相干效应，在物体下表面而形成一定的amplitude contrast.进而出射波通过透镜传递到像平面，包括phase和amplitude又都再次受到了球差的影响从而形成了最终的像衬度。

这样一来，显然球差校正的显微镜因为有更高的分辨率从而有优势。