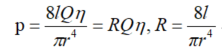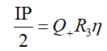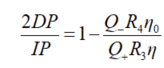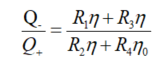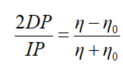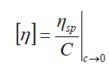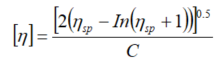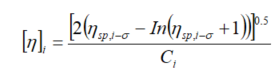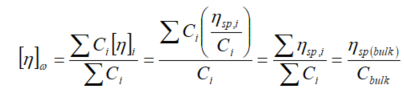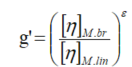主题：【第十二届原创】趣谈凝胶渗透色谱GPC/SEC– 检测篇III粘度检测器

终于聊到了粘度检测器，博士刚刚接触的时候觉得这是GPC检测器中最复杂也是最有意思的检测器，事实证明，确实如此！
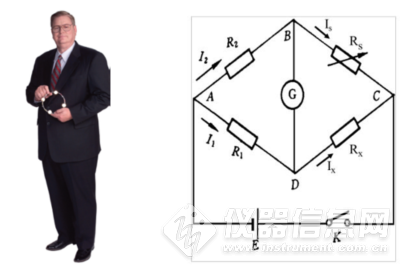
好多故事，我们从GPC在线粘度检测器的起源聊起吧。话说1983年的时候，美国的MaxHaney博士（下图）在一个很大的石化公司实验室中做实验。很经典但很无聊的实验，使用乌式毛细管粘度计测粘度，一边盯着超级恒温槽中粘度计液面一手拿着一个秒表计时。有多无聊？一个高分子溶液配置若干浓度，检测每一个溶液的相对粘度，然后换算成增比粘度，然后多点外推得到特性粘度，然后利用Mark-Houwink方程计算粘均分子量，然后，再继续检测下一个样品……啊，这日子没法过了。


Max经常思维奔逸（褒义词啊），一天他看到了一个电路- 惠斯通电桥（上图）。通过惠斯通电桥可以准确检测电路的电阻。咦？既然这样的话，粘度不也是一种阻力吗？把导线换成流路岂不是可以检测溶液的粘度？Max相当兴奋，他第一时间把这个想法告诉了他的老板，但，他的老板不Care！并，希望他回到岗位继续看表测粘度。真绝望啊！
要说一个成功男人的背后，基本都有一个伟大的女人。这个女人就是Max的老婆。回家后，Max和他太太诉说了心中的苦闷，他太太对于他的想法非常支持，并鼓励他把想法变为现实。于是，出现了与凝胶色谱连用的四毛细管粘度检测器（84年），于是出现了ViscotekCo，于是Max的老板成了他的第一个客户。
历史上曾经出现过不同设计的GPC粘度检测器，有W公司的三毛细管设计也有D公司的双毛细管设计，但事实证明，Max的四毛细管设计最为成功，在灵敏度和稳定性以及桥路平衡上实现了性能的最优，并成为唯一延续下来的经典。


特性粘度和在线粘度检测器工作原理
微分粘度计—设计


GPC在线粘度检测器再使用的过程中必须与一个浓度检测器一起连用，以提供每个流出组分的浓度信息，大部分时候是RI检测器。由于粘度检测器需要分流，在检测器序列中需要放在最后，而RI检测器的耐压性最差也需要放在最后，所以大部分公司的RI和粘度采用并联。也有公司例外，采用串联并把RI放在前端，但是RI必须进行良好的过压保护。
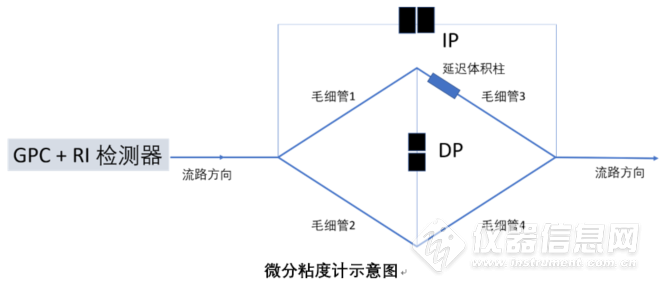
常见的微分粘度计采用的是Haney发明的四毛细管桥路结构。如图所示，四根内径相同的毛细管（R1-R4）以与电路中常见的惠斯通电桥类似的平衡式桥路结构。微分压力传感器测量桥路中点（DP）的压力差以及入口与出口间（IP）的压力差。在毛细管R4上有一段延迟体积腔，它是测定高分子样品洗脱液时，用来提供溶剂经过R4毛细管的参比。此延迟体积腔应当满足以下要求：
1.延迟体积腔的容量必须大于GPC柱的净洗脱量。
2.延迟体积腔内的流阻必须远小于毛细管阻力。
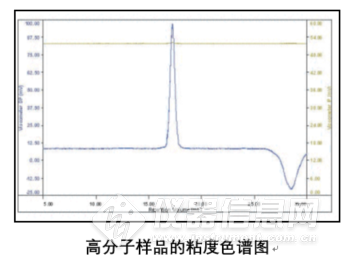
此外选用的毛细管其流阻应基本一致，使DP处的压力差为零，而且能使色谱泵引起的脉冲也相互抵消。下图所示，当样品从GPC被洗脱后，DP处的测量结果与样品粘度相关。图中第一个峰是当样品溶液流经毛细管R1、R2及R3，而溶剂流过毛细管R4时测得的。第二个倒峰是由延迟体积腔内的样品被冲洗进入R4引起的。此时，毛细管R4内流过的是样品溶液，而其他三根毛细管内则是溶剂。在计算过程中并不需要对这个峰进行分析。

微分粘度计—原理

伯努利方程描述了流体流经管路的变化情况，其进出口压力差与流速Q，粘度η与阻率R有关。

如上图所示，DP处的信号等于流体流经管R3的压力差减去流经管R4和延迟体积的压力差。图中的第一个峰，在样品的洗脱过程中，由伯努利方程可以得到DP处测量值为：

式中，Q₊指正回路的流速，Q_-指逆回路的流速，η是样品的粘度，η₀是溶剂的粘度。类似的，IP点的测量值也可以用下式表示：

用上上式除以上式可以得到：

两回路流速之比可以用每个回路的相对阻力计算：

这里需要假设所有毛细管流阻都相同。


结合式上上式与上式可得到与样品粘度η和溶剂粘度η₀相关的表达式：

溶液比粘度即为：

将上式代入上上式，可得到微分粘度计的基本方程：

粘度函数
微分粘度计能够准确灵敏的测量洗脱的高分子样品的比粘度。不过，我们的目标是要测得特性粘度，它是理论上无限稀释样品的比粘度与浓度的比值。

特性粘度传统的计算方法是通过外推得到当浓度为零时η_sp/C的比值。然而在色谱检测中，没有办法也没有必要运用这种方法。对于可用于低浓度范围的GPC方法，Solomon等人指出特性粘度的单点估计已经足够准确。

之前部分中，已介绍折光系数检测法可以计算色谱洗脱液的浓度曲线C_i。在第二部分中，将光散射检测器与RI检测器联用则能计算色谱洗脱的分子量曲线。根据上上式的定义，同样也可以得到色谱的比粘度曲线，而粘度曲线可以由下式取得：

重均特性粘度的测量非常有价值，它代表了样品整体的特性粘度。可用传统的玻璃毛细管粘度计测量。有下面的推导证明：


在线粘度检测器表征分子结构

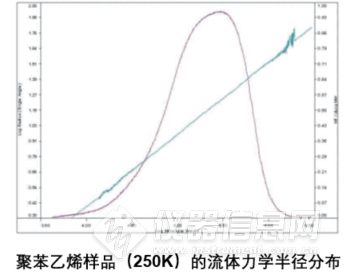
应用——流体力学半径
爱因斯坦揭示了溶液粘度与溶液中颗粒的流体力学半径有关。

Φ是溶液中总悬浮物体积中颗粒的体积分数。将其转化为浓度单位后，可与特性粘度、分子量以及流体力学半径有如下关系：


如果是三检测联用的GPC/SEC可以测量特性粘度与绝对分子量，进而得到R_h的绝对量，这对高分子研究十分有用。上图中是测得的R_h以及质量分数分布图。很明显在样品的整个分布范围内R_h能够被精确测量。
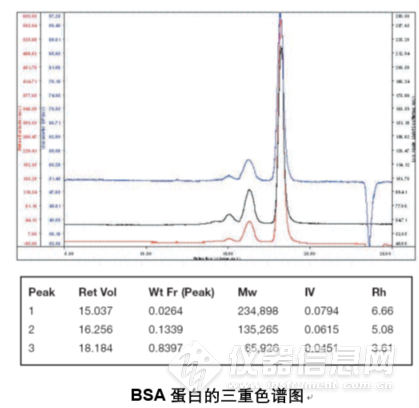
R_h的测量对表征蛋白质尤其有应用价值。如下图所示，单体、二聚体以及三聚体能分别被准确的计算出来。


应用——支化
高分子的长链支化度与特性粘度可以通过下式关联：

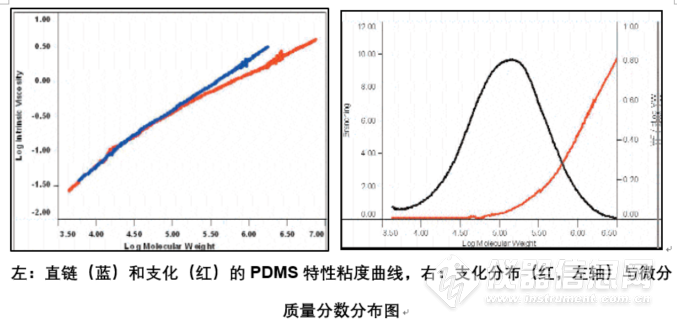
_M,br代表了支化高分子当其分子量为M时的特性粘度，而_M,lin是在分子量为M时直链高分子的特性粘度。ε是与结构有关的一个参数，其平均值约为0.8。下图中是一个支链计算的实例。下图左边是直链与支化的聚二甲基硅氧烷（PDMS）高分子样品以特性粘度对分子量作图得到的Mark-Houwind曲线。尽管在这类高分子中支化的数量不大，Mark-Houwink曲线依然清晰地表明支化分子与直链分子的区别。在上式中的g’可由此计算。下图右边中是支化PDMS样品的质量分数分布以及支化分布。左侧坐标轴是支链的数目，其范围涵盖了从无支链的低分子量，在一百万道尔顿分子量时平均4个支链的，以及在最高的分子量平均每分子8个支链。

Mark-Houwink曲线
粘度计检测器还可以提供如分子构造、聚合以及支化等重要的结构信息。由上文可知，通过GPC的粘度检测器能够直接测量高分子样品的特性粘度，而特性粘度是溶液中高分子的密度倒数。作为一个直接而灵敏的结构参数，特性粘度也是高分子工业中的传统重要参数。
著名的Mark-Houwink曲线：

可通过特性粘度对分子量作双对数图得到。Mark-Houwink曲线是高分子结构分析中的重要曲线。它反映了高分子的结构变化，例如支化度或链刚性。其斜率是Mark-Houwink方程中的a，范围在0-2之间，当分子是固球体时为0，柱形结构时为2。
    Mark-Houwink曲线斜率的变化可用来判断是否有支化发生。
结论
粘度计检测器是三检测联用中最后的一个重要部分。我们已经介绍了使用RI检测器准确测定浓度曲线以及使用光散射技术准确测定分子量。粘度计检测器则能够测定所有重要的结构信息，使GPC/SEC能够用于测定高分子的支化程度或者的蛋白质的流体力学尺寸差异。这是三种不同的检测器完美组合达到的功能，而非任何单一或者双重的检测器能够实现。

普氏校正UniversalCalibration表征高分子真实分子量及其分布

在传统校准法的帖子中，当被测样品与用于校准的标样化学性质有区别时会导致误差的产生，并且这在日常实验中经常发生。因此，可以通过额外联用一个检测器（如四毛细管微分粘度计）对传统校准法进行改进，这就是普适校准法。
普适校准式1967年的时候Benoit发现的一个现象而诞生的。当时，Benoit发现如果在分子量的基础上引入特性粘度，即Mw*IV，那么不同种类高分子的流出校正曲线会重合在一起。后面理论证实了，Mw*IV正比于分子体积Vh，这就解释了这个现象，因为GPC本身就是按照分子体积而不是分子量进行分离的。
粘度检测器最早应用于普适校准法。普适校准法是一种色谱柱校准方法，不要求标样和被检测的样品具有相同分子结构。当分子量很低或者dn/dc值较小时，这种方法依然可以应用。但是，对于大部分的高分子，光散射技术测定分子量是较好的选择。粘度检测器同时也可以测量高分子的其他性质，尤其是与体积和结构有关的性质，因此三检测联用系统是本技术的发展趋势。下面将介绍两个检测器联用系统的应用实例。
正如之前所描述的，GPC的原理是通过大分子的流体力学半径或流体力学体积进行分离。因此，要准确校准色谱柱，需要在流体力学体积与保留时间之间找到关联（如通用校准法），而非分子量与保留体积之间（如传统校准法）。联用粘度计检测器可以实现这个目的。它能够直接测量特性粘度，而特性粘度与高分子的分子密度是成反比的。
分子质量与特性粘度的乘积与流体力学体积有如下关系：
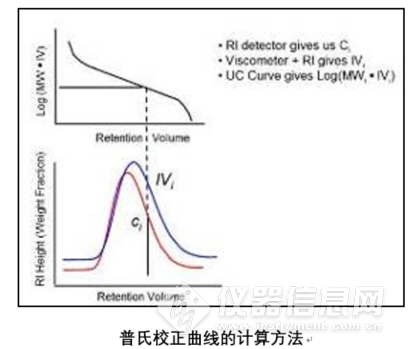
MW • IV = 5/2 • N_A • V_h
由于粘度计检测器通常与浓度检测器（RI或UV/VIS）联用可以直接测量特性粘度（IV），所以我们就可以Log(V_h)对保留体积（RV）作图得到校准曲线。
具体步骤如下所示：
1.分子量已知的窄分布系列样品进样
2.测量信号峰的保留体积
3.根据信号峰计算IV
4.以Log(V_h)对保留体积（Rv）作图得到校准曲线

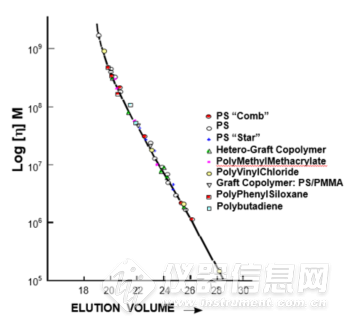
普氏校正曲线，所有种类的标准样品都落在以分子体积-流出时间为坐标的一条曲线上

由此，在分析未知样品时，RV_i的每个数据点都可以通过校准曲线找到Y = Log(Mw_i • IV_i)。由于使用了粘度计计算IV_i，可推导得到Mw_i =10^Y/ IV_i.

综上所述，我们就能使用在传统校准法中推导的公式来计算Mn，Mw与Mz均值。
好了，祝大家生活愉快，身体健康！