主题：【求助】判定规则和符合性声明

原文由 路云(luyunnc) 发表:
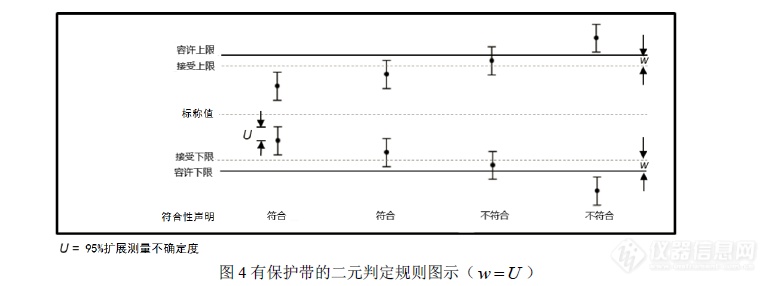
  个人觉得，“接受上限”应该比“容许上限”更严苛，而不是更宽松。举个例子来说，某零件尺寸要求为(10.0±1.0) mm。那么该零件尺寸的“容许上限”就是11.0 mm。假如最终的测得值是10.9 mm，不确定度U＝0.2 mm。此时，测得值的实际值，是以约95 %概率，落在以10.9 mm为中心的±0.2 mm的区间范围内(即10.7 mm～11.1 mm)。此时，如果你对10.9 mm的测量结果判定为合格，那么就存在误判的风险，因为测得值的实际值完全有可能落在11.0 mm～11.1 mm之间的不合格区间。
  那么怎么样才能避免误判的风险呢？简单的办法就是缩小“接受区间”，即：将“接受上限”定在10.8 mm(容许上限－U＝11.0 mm－0.2 mm＝10.8 mm)。这样，当测得值不大于10.8 mm时，判定合格就不存在有误判的风险了(注：只讨论上限要求，不包括下限要求)。即使有风险，其风险的程度也小于5 %(因为U的置信概率就是约95 %)。

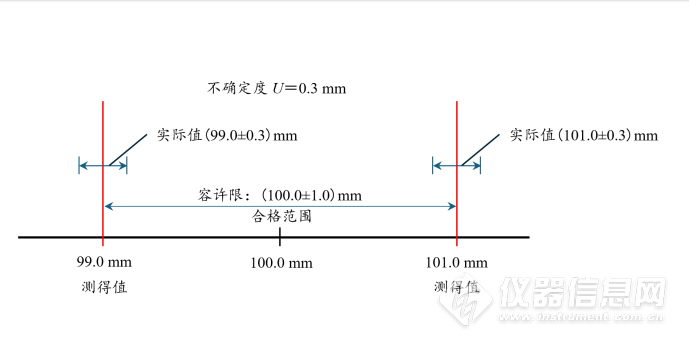
原文由 Ins_1065932a(Ins_1065932a) 发表:
那请问，容许上限和接受上限，和客户提供的判定标准上限值有什么区别呢，我来自第三方检测机构。

原文由 路云(luyunnc) 发表:
      您要看客户提供的判定标准上限，是不是与产品标准的容许上限一致。如果一致，那么客户就是将容许上限作为接受上限。

原文由 Ins_1065932a(Ins_1065932a) 发表:
谢谢老师回复。“被测量值服从对称正态分布时，当测得值正好落在容许限上时，做出错误判定的概率高达50%”，请问这个50%的概率是怎么得来的呢？谢谢。

原文由 路云(luyunnc) 发表:
      因为“测量结果的不确定度”是以“测得值”为中心的对称区间半宽度。所以当“测得值”刚好落在容许限上(落在容许上限上，或落在容许下限上)时，不确定度的区间正好一半在容许区间内，一半在容许区间外，所以误判的概率就是50 %。举个例子来说，可能更容易理解。假设某被测零件的长度要求是(100.0±1.0) mm，也就是说容许上限是101.0 mm，容许下限是99.0 mm。假如实际的“测得值”正好落在容许限上，是101.0 mm(或99.0 mm)，且“测得值”的不确定度U＝0.3 mm(假设为正态分布)。我们来看看，此时给出的“测得值”实际上是“最佳估计值”，或者说是一组测量结果的“平均值”。不确定度U＝0.3 mm就表明，“实际值”是以正态分布的形态，以一定的概率分布在以“测得值”为中心，以U＝0.3 mm为半宽度的对称区间范围内，即“实际值”落在“测得值”101.0 mm±0.3 mm(或“测得值”99.0 mm±0.3 mm)范围内。此时不难看出，“实际值”落在容许限内(99.0 mm～99.3 mm，或100.7 mm～101.0 mm)的区间大小，与落在容许限外(98.7 mm～99.0 mm，或101.0 mm～101.3 mm)的区间大小是一样的。所以说当“测得值”正好落在容许限上时，无论你是判“合格”还是判“不合格”，误判的概率都是一样的，各占50 %。

原文由 路云(luyunnc) 发表:
      因为“测量结果的不确定度”是以“测得值”为中心的对称区间半宽度。所以当“测得值”刚好落在容许限上(落在容许上限上，或落在容许下限上)时，不确定度的区间正好一半在容许区间内，一半在容许区间外，所以误判的概率就是50 %。举个例子来说，可能更容易理解。假设某被测零件的长度要求是(100.0±1.0) mm，也就是说容许上限是101.0 mm，容许下限是99.0 mm。假如实际的“测得值”正好落在容许限上，是101.0 mm(或99.0 mm)，且“测得值”的不确定度U＝0.3 mm(假设为正态分布)。我们来看看，此时给出的“测得值”实际上是“最佳估计值”，或者说是一组测量结果的“平均值”。不确定度U＝0.3 mm就表明，“实际值”是以正态分布的形态，以一定的概率分布在以“测得值”为中心，以U＝0.3 mm为半宽度的对称区间范围内，即“实际值”落在“测得值”101.0 mm±0.3 mm(或“测得值”99.0 mm±0.3 mm)范围内。此时不难看出，“实际值”落在容许限内(99.0 mm～99.3 mm，或100.7 mm～101.0 mm)的区间大小，与落在容许限外(98.7 mm～99.0 mm，或101.0 mm～101.3 mm)的区间大小是一样的。所以说当“测得值”正好落在容许限上时，无论你是判“合格”还是判“不合格”，误判的概率都是一样的，各占50 %。